実験 計画 法 3 因子 3 水準 17++ Ideas in 2022
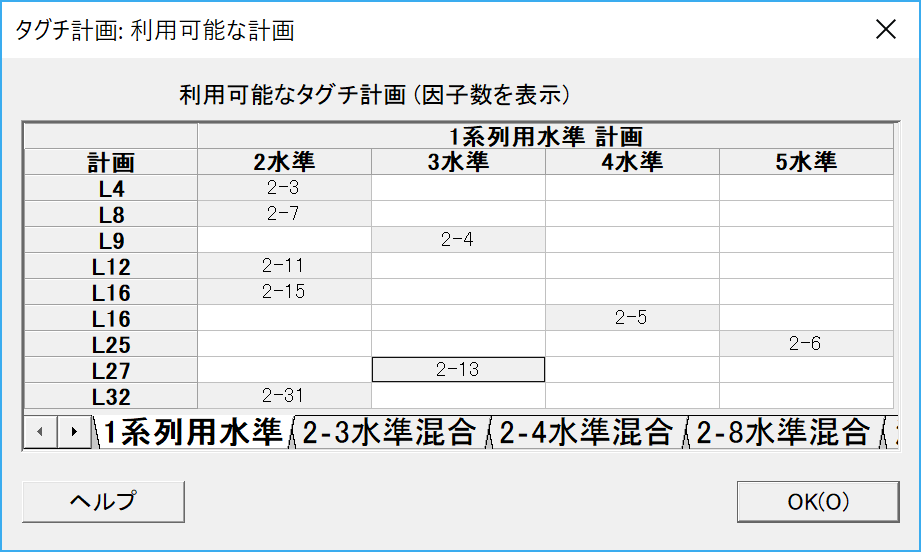
実験 計画 法 3 因子 3 水準. 2水準計画、3水準計画、4水準計画、5水準計画、混合水準計画が含まれます。 実験の要件に基づいて適切な計画を選択します。 [統計] > [実験計画法(doe)] メニューから計画を選択します。 Experimental design、design of experiments )は、効率のよい実験方法を設計(デザイン)し、結果を適切に解析することを目的とする統計学の応用分野である。 r・a・フィッシャーが1920年代に農学試験から着想して発展させた。 。特に1950年g・m・コックスとw・g. 3因子交互作用という。交互作用を表すのには×の記号を使う。例として、 aとbとの2因子交互作用はaxbで表すー。 前頁で述べた単一因子実験法は、とりあげた因子聞に交互作用が存在する 場合にはよい実験法ではない。 11 i j' 11 11 j' 3水準直交表 実験の因子(パラメータ)のどの2つをとっても、その水準のすべての組み合わせが同数回現れるように作成したものが直交表でした。 [math] \displaystyle n=2 [/math]のラテン方格は下記の通りで、 最小の2水準直交表[math] \displaystyle l4 [/math]と同一で. B 1, b 2, b 3 ・時間100,200,300min: A 1, a 2, a 3 ・圧力1.0,1.5,2.0atm: C 1, c 2, c 3 3.因子の右下に水準を表記します. 直交計画も, ラテン方格のように実験回数を減らして効率的に実験を設計する方法。 因子の数を4個として, 各水準を3とすると, 4^3 = 64回となるが, このような場合に直交計画は現実的に実施可能な範囲 (最低限の直交性を維持したまま) に保ちながら, できる. (*)多水準作成法で4水準を作り、擬水準法で3水準に落とす(1, 2, 2’, 3)。3水準の因子が 2個以上ある場合には、擬水準から求まる誤差(アソビ列)をダブらせる。 11 2.2 多水準作成法・アソビ列法・擬水準法・変身法(続き) (3)擬水準法 3水準系の直交表を. 因子と水準の組合せ (解説) 1.因子と水準の組合せについて、説明して行きます。 2.因子と水準の組合せは、下記の様になります。 ・温度100,110,120℃ :
A 1, a 2, a 3 ・圧力1.0,1.5,2.0atm: (*)多水準作成法で4水準を作り、擬水準法で3水準に落とす(1, 2, 2’, 3)。3水準の因子が 2個以上ある場合には、擬水準から求まる誤差(アソビ列)をダブらせる。 11 2.2 多水準作成法・アソビ列法・擬水準法・変身法(続き) (3)擬水準法 3水準系の直交表を. 直交計画も, ラテン方格のように実験回数を減らして効率的に実験を設計する方法。 因子の数を4個として, 各水準を3とすると, 4^3 = 64回となるが, このような場合に直交計画は現実的に実施可能な範囲 (最低限の直交性を維持したまま) に保ちながら, できる. 因子と水準の組合せ (解説) 1.因子と水準の組合せについて、説明して行きます。 2.因子と水準の組合せは、下記の様になります。 ・温度100,110,120℃ : 3因子交互作用という。交互作用を表すのには×の記号を使う。例として、 aとbとの2因子交互作用はaxbで表すー。 前頁で述べた単一因子実験法は、とりあげた因子聞に交互作用が存在する 場合にはよい実験法ではない。 11 i j' 11 11 j' B 1, b 2, b 3 ・時間100,200,300min: Experimental design、design of experiments )は、効率のよい実験方法を設計(デザイン)し、結果を適切に解析することを目的とする統計学の応用分野である。 r・a・フィッシャーが1920年代に農学試験から着想して発展させた。 。特に1950年g・m・コックスとw・g. 2水準計画、3水準計画、4水準計画、5水準計画、混合水準計画が含まれます。 実験の要件に基づいて適切な計画を選択します。 [統計] > [実験計画法(doe)] メニューから計画を選択します。 C 1, c 2, c 3 3.因子の右下に水準を表記します. 3水準直交表 実験の因子(パラメータ)のどの2つをとっても、その水準のすべての組み合わせが同数回現れるように作成したものが直交表でした。 [math] \displaystyle n=2 [/math]のラテン方格は下記の通りで、 最小の2水準直交表[math] \displaystyle l4 [/math]と同一で.
実験 計画 法 3 因子 3 水準 (*)多水準作成法で4水準を作り、擬水準法で3水準に落とす(1, 2, 2’, 3)。3水準の因子が 2個以上ある場合には、擬水準から求まる誤差(アソビ列)をダブらせる。 11 2.2 多水準作成法・アソビ列法・擬水準法・変身法(続き) (3)擬水準法 3水準系の直交表を.
3水準直交表 実験の因子(パラメータ)のどの2つをとっても、その水準のすべての組み合わせが同数回現れるように作成したものが直交表でした。 [math] \displaystyle n=2 [/math]のラテン方格は下記の通りで、 最小の2水準直交表[math] \displaystyle l4 [/math]と同一で. (*)多水準作成法で4水準を作り、擬水準法で3水準に落とす(1, 2, 2’, 3)。3水準の因子が 2個以上ある場合には、擬水準から求まる誤差(アソビ列)をダブらせる。 11 2.2 多水準作成法・アソビ列法・擬水準法・変身法(続き) (3)擬水準法 3水準系の直交表を. 因子と水準の組合せ (解説) 1.因子と水準の組合せについて、説明して行きます。 2.因子と水準の組合せは、下記の様になります。 ・温度100,110,120℃ : A 1, a 2, a 3 ・圧力1.0,1.5,2.0atm: C 1, c 2, c 3 3.因子の右下に水準を表記します. B 1, b 2, b 3 ・時間100,200,300min: 直交計画も, ラテン方格のように実験回数を減らして効率的に実験を設計する方法。 因子の数を4個として, 各水準を3とすると, 4^3 = 64回となるが, このような場合に直交計画は現実的に実施可能な範囲 (最低限の直交性を維持したまま) に保ちながら, できる. 3因子交互作用という。交互作用を表すのには×の記号を使う。例として、 aとbとの2因子交互作用はaxbで表すー。 前頁で述べた単一因子実験法は、とりあげた因子聞に交互作用が存在する 場合にはよい実験法ではない。 11 i j' 11 11 j' 2水準計画、3水準計画、4水準計画、5水準計画、混合水準計画が含まれます。 実験の要件に基づいて適切な計画を選択します。 [統計] > [実験計画法(doe)] メニューから計画を選択します。 Experimental design、design of experiments )は、効率のよい実験方法を設計(デザイン)し、結果を適切に解析することを目的とする統計学の応用分野である。 r・a・フィッシャーが1920年代に農学試験から着想して発展させた。 。特に1950年g・m・コックスとw・g.
3因子交互作用という。交互作用を表すのには×の記号を使う。例として、 AとBとの2因子交互作用はAxbで表すー。 前頁で述べた単一因子実験法は、とりあげた因子聞に交互作用が存在する 場合にはよい実験法ではない。 11 I J' 11 11 J'
因子と水準の組合せ (解説) 1.因子と水準の組合せについて、説明して行きます。 2.因子と水準の組合せは、下記の様になります。 ・温度100,110,120℃ : 2水準計画、3水準計画、4水準計画、5水準計画、混合水準計画が含まれます。 実験の要件に基づいて適切な計画を選択します。 [統計] > [実験計画法(doe)] メニューから計画を選択します。 Experimental design、design of experiments )は、効率のよい実験方法を設計(デザイン)し、結果を適切に解析することを目的とする統計学の応用分野である。 r・a・フィッシャーが1920年代に農学試験から着想して発展させた。 。特に1950年g・m・コックスとw・g.
B 1, B 2, B 3 ・時間100,200,300Min:
A 1, a 2, a 3 ・圧力1.0,1.5,2.0atm: (*)多水準作成法で4水準を作り、擬水準法で3水準に落とす(1, 2, 2’, 3)。3水準の因子が 2個以上ある場合には、擬水準から求まる誤差(アソビ列)をダブらせる。 11 2.2 多水準作成法・アソビ列法・擬水準法・変身法(続き) (3)擬水準法 3水準系の直交表を. 3水準直交表 実験の因子(パラメータ)のどの2つをとっても、その水準のすべての組み合わせが同数回現れるように作成したものが直交表でした。 [math] \displaystyle n=2 [/math]のラテン方格は下記の通りで、 最小の2水準直交表[math] \displaystyle l4 [/math]と同一で.
C 1, C 2, C 3 3.因子の右下に水準を表記します.
直交計画も, ラテン方格のように実験回数を減らして効率的に実験を設計する方法。 因子の数を4個として, 各水準を3とすると, 4^3 = 64回となるが, このような場合に直交計画は現実的に実施可能な範囲 (最低限の直交性を維持したまま) に保ちながら, できる.